Is there a name for when someone thinks they are really bad at something (for example math) and they have learned not to trust their own intuition at all so they make really wild errors by second guessing themselves?
-
Using color to identify angles means you can't use it to show which ones are the same. Which is a great use for color if you don't have color blind students. (I don't at the moment but it's always in the back of my mind. )
@futurebird @jetlagjen ps this is the system of arcs I was talking about, to identify which angles are the same size. It works pretty well until you have a more complicated shape with many angles. Is there a name for this system?
-
@futurebird @3TomatoesShort @EverydayMoggie But why use a compass to do that? Why not a ruler through the middle?
@Bumblefish @3TomatoesShort @EverydayMoggie
Rulers are less precise than a compass. You could use a ruler if you wanted. But it will only be as precise as the markings you have made on the ruler.
-
@Bumblefish @3TomatoesShort @EverydayMoggie
Rulers are less precise than a compass. You could use a ruler if you wanted. But it will only be as precise as the markings you have made on the ruler.
@futurebird @3TomatoesShort @EverydayMoggie Not measuring anything, just using it to get a straight line. Could use any straight edge.
-
@futurebird @3TomatoesShort @EverydayMoggie But why use a compass to do that? Why not a ruler through the middle?
@Bumblefish @3TomatoesShort @EverydayMoggie
This is a very deep mathematical question in a way. Why do we do geometric constructions with a "straight edge" and compass and not a ruler and compass?
-
@futurebird @jetlagjen ps this is the system of arcs I was talking about, to identify which angles are the same size. It works pretty well until you have a more complicated shape with many angles. Is there a name for this system?
We use this system, but asking which angles are the same when they are marked like this isn't testing the concept I'm getting at.
It's called "decoration" or "tic marks" and the little marks on the sides of the original triangle I posted are a part of the same system.
I would expect a student to mark the angles like this based on the way the sides are marked. My struggling student would make the wrong two the same.
-
@futurebird @3TomatoesShort @EverydayMoggie Not measuring anything, just using it to get a straight line. Could use any straight edge.
@Bumblefish @3TomatoesShort @EverydayMoggie
But how would you get the angle at the center exactly the same with just ruler?
-
@Bumblefish @3TomatoesShort @EverydayMoggie
But how would you get the angle at the center exactly the same with just ruler?
@futurebird @3TomatoesShort @EverydayMoggie Wherever the cross happens is the peak of the triangle.
-
@futurebird @3TomatoesShort @EverydayMoggie Wherever the cross happens is the peak of the triangle.
@Bumblefish @3TomatoesShort @EverydayMoggie
The peak is the angle at the center, right? I don't see a "cross"
-
@Bumblefish @3TomatoesShort @EverydayMoggie
The peak is the angle at the center, right? I don't see a "cross"
@futurebird @3TomatoesShort @EverydayMoggie That’s because you haven’t drawn one and for the life of me I don’t know why. You need the cross to cut the pizza.
-
@futurebird @3TomatoesShort @EverydayMoggie That’s because you haven’t drawn one and for the life of me I don’t know why. You need the cross to cut the pizza.
@Bumblefish @3TomatoesShort @EverydayMoggie
OK great. I still don't see how to cut two slices that are the same size from the identical circles without measuring with the ruler or using the compass again.
-
@Bumblefish @3TomatoesShort @EverydayMoggie
OK great. I still don't see how to cut two slices that are the same size from the identical circles without measuring with the ruler or using the compass again.
@futurebird @3TomatoesShort @EverydayMoggie The opposite one will always be the same size.
-
@futurebird @3TomatoesShort @EverydayMoggie The opposite one will always be the same size.
@Bumblefish @3TomatoesShort @EverydayMoggie
Absolutely.
But if you want to copy an angle to a new location that won't help.
-
@Bumblefish @3TomatoesShort @EverydayMoggie
Absolutely.
But if you want to copy an angle to a new location that won't help.
@futurebird @3TomatoesShort @EverydayMoggie Tracing paper FTW!
-
@futurebird @3TomatoesShort @EverydayMoggie Tracing paper FTW!
@Bumblefish @3TomatoesShort @EverydayMoggie
Tracing paper isn't really making a copy. It's just the same figure again. As I see it anyways.
But my point here is that it take two "measurements" with these tools.
I'm going to use some of this I think. Very cool stuff.
-
Is there a name for when someone thinks they are really bad at something (for example math) and they have learned not to trust their own intuition at all so they make really wild errors by second guessing themselves?
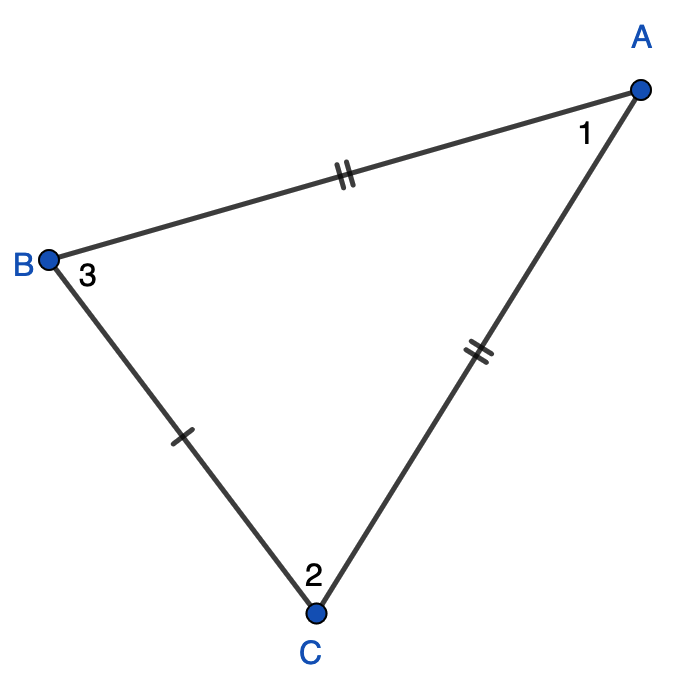
Here is a question:
Which angles are equal?To me this is an "easy" question even if you don't know about isosceles triangles or anything. The symmetry of the figure suggests that 3 and 2 are congruent.
I have a student who is struggling with this kind of thing.
If I saw the numbers *inside* the angles as a kid, I would have said they are not equal. That has nothing to do with the measurements of said angles, which match. I'm struggling to view them as equal as an adult.
Descriptive mathematical statements in English are their own dialect, but are not treated as such by people who use math when interacting with people who don't speak that dialect.
Question is easy, meaning derived from phrasing is hard.
-
If I saw the numbers *inside* the angles as a kid, I would have said they are not equal. That has nothing to do with the measurements of said angles, which match. I'm struggling to view them as equal as an adult.
Descriptive mathematical statements in English are their own dialect, but are not treated as such by people who use math when interacting with people who don't speak that dialect.
Question is easy, meaning derived from phrasing is hard.
This is why basic math and esp. geometry were hard for me, but algebra was easy.
I had two math teachers in a room describe what they said was the same solution to the same problem, but I heard two different problems, solutions, and answers. They were both very exacting about what was the right answer, but became flustered when I brought up what didn't match up for me. In this thread, I've seen multiple notations for the same thing. To me, they are all different problems.
-
This is why basic math and esp. geometry were hard for me, but algebra was easy.
I had two math teachers in a room describe what they said was the same solution to the same problem, but I heard two different problems, solutions, and answers. They were both very exacting about what was the right answer, but became flustered when I brought up what didn't match up for me. In this thread, I've seen multiple notations for the same thing. To me, they are all different problems.
The things that are the same are what we are really trying to talk about.
-
The things that are the same are what we are really trying to talk about.
Ok. Sorry for being offbase.
-
Ok. Sorry for being offbase.
I didn't mean that you were off base. (Nor do I think you have anything to apologize for. )
It's fine to prefer a certain notation ... but the notation isn't really what it's about. I'm just suggesting that as a thread to pull to get past what isn't as important here.
I'm very particular about notation because I know it can be confusing as I explain here:
myrmepropagandist (@futurebird@sauropods.win)
@jetlagjen@gts.phillipsuk.org We use the numbers consistently because I find using three letters is more confusing for most students. eg ∠ABC = ∠BCA vs. ∠3 = ∠2 Which do you find less confusing? We could also do ∠B = ∠C but naming angles by single letter is a bad habit since there can be multiple angles at a vertex.

Sauropods.win (sauropods.win)