Is there a name for when someone thinks they are really bad at something (for example math) and they have learned not to trust their own intuition at all so they make really wild errors by second guessing themselves?
-
One of the harder things to accept as a teacher is that some kids will just never like math. That's fine though. I can cope.
What everyone *can* like (at least) is getting the right answer and knowing it's right. Knowing that yourself not needing anyone to tell you.
So I'm hoping we can at least get to that stage.
Right now I think she thinks I'm just making up geometry as I go and it's basically Calvinball.
Maybe it's not any of those things; it could be that she just can't see the symmetry. Brains can have all kinds of weird gaps in visual-spatial understanding.
-
@futurebird it is possible that she just doesn't good spatial “awareness” (I'm not sure that's the right term?) rather than lack of trust, although this doesn't make it any easier to tell how much of it is nature and how much is (lack of) nurture. She wouldn't be the first person I know of with excellent abstract reasoning skill and no spatial intuition anyway.
(That being said, verifying the intuition even when the answer is obvious is a Good Habit
 for a mathematician 8-D)
for a mathematician 8-D)To be honest I don't really know. I've known her for only a few months and she's working very hard, possibly too hard to keep up. I'm worried she has some horrible complex system to either compensate or avoid dealing with the spatial reasoning.
I have the students work with compasses and it helps some of them. The compass is her mortal enemy. Every time she places it, it's just a guess ...
-
Is there a name for when someone thinks they are really bad at something (for example math) and they have learned not to trust their own intuition at all so they make really wild errors by second guessing themselves?
Here is a question:
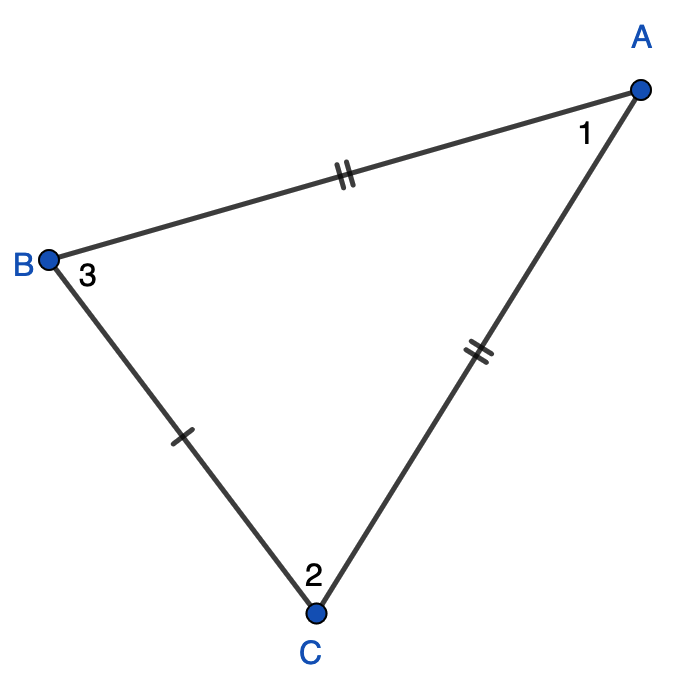
Which angles are equal?To me this is an "easy" question even if you don't know about isosceles triangles or anything. The symmetry of the figure suggests that 3 and 2 are congruent.
I have a student who is struggling with this kind of thing.
@futurebird the ”i’m bad at math” fallacy is incredibly common.
My ex kept saying to so much to my kid, I have had to keep fixing that assumption all her life, with no end in sight.
-
@futurebird the ”i’m bad at math” fallacy is incredibly common.
My ex kept saying to so much to my kid, I have had to keep fixing that assumption all her life, with no end in sight.
Very very few people are really "bad at math" in any real sense of the phrase. It's possible... but most of the time it's more like "had bad experiences being wrong and now avoid it" or "it's tedious and I have other things to do"
-
Very very few people are really "bad at math" in any real sense of the phrase. It's possible... but most of the time it's more like "had bad experiences being wrong and now avoid it" or "it's tedious and I have other things to do"
@futurebird one bad teacher might be all they need
-
@futurebird one bad teacher might be all they need
Sometimes you can learn a LOT from a bad teacher. But that tends to come later in ones education.
(thinking of my analysis teacher in college. good lord. )
-
Maybe it's not any of those things; it could be that she just can't see the symmetry. Brains can have all kinds of weird gaps in visual-spatial understanding.
@EverydayMoggie
I was thinking this - I can see it, but it's not *super* obvious to me. I think if I was a young'un just starting out in math, I would want to cut it out and fold it in half to check
(Ooh though I remember now we had little mirror thingies to check, too?)
@futurebird -
@EverydayMoggie
I was thinking this - I can see it, but it's not *super* obvious to me. I think if I was a young'un just starting out in math, I would want to cut it out and fold it in half to check
(Ooh though I remember now we had little mirror thingies to check, too?)
@futurebird@3TomatoesShort @EverydayMoggie @futurebird I was going to suggest paper modeling. I can’t calculate anything to save my life, but give me a concrete thing I can shape with my hands and things start to make sense. You mentioned compasses. Nobody has reliably convinced me they can do anything except make circles. The whole thing where you use them to make angles is deep magic that only wizards can perform.
-
Is there a name for when someone thinks they are really bad at something (for example math) and they have learned not to trust their own intuition at all so they make really wild errors by second guessing themselves?
Here is a question:
Which angles are equal?To me this is an "easy" question even if you don't know about isosceles triangles or anything. The symmetry of the figure suggests that 3 and 2 are congruent.
I have a student who is struggling with this kind of thing.
@futurebird this is the sort of thing I usually find easy, but it threw me for a second. Then I realised the numbers were *labels* and not any kind of measurement.
-
@futurebird this is the sort of thing I usually find easy, but it threw me for a second. Then I realised the numbers were *labels* and not any kind of measurement.
We use the numbers consistently because I find using three letters is more confusing for most students.
eg ∠ABC = ∠BCA
vs. ∠3 = ∠2
Which do you find less confusing?
We could also do ∠B = ∠C but naming angles by single letter is a bad habit since there can be multiple angles at a vertex.
-
Is there a name for when someone thinks they are really bad at something (for example math) and they have learned not to trust their own intuition at all so they make really wild errors by second guessing themselves?
Here is a question:
Which angles are equal?To me this is an "easy" question even if you don't know about isosceles triangles or anything. The symmetry of the figure suggests that 3 and 2 are congruent.
I have a student who is struggling with this kind of thing.
@futurebird
Back in the last century I did some simple research for a professional development certificate (I was a Design Tech teacher). It arose when I was teaching an electronics module I found a lot of students confused about up/down, left/right, rotate/flip. I'd give out 20 printed circuit boards and get the kids to hold them so they could see the school logo right way up. (Printed on the circuit track side). Then demo flipping l-r to the blank side where they would insert components(cont) -
@futurebird
Back in the last century I did some simple research for a professional development certificate (I was a Design Tech teacher). It arose when I was teaching an electronics module I found a lot of students confused about up/down, left/right, rotate/flip. I'd give out 20 printed circuit boards and get the kids to hold them so they could see the school logo right way up. (Printed on the circuit track side). Then demo flipping l-r to the blank side where they would insert components(cont)I'm trying to understand this.
If I flip a board "l-r" will the result be different than "r-l" ?
The way I'm picturing this the answer would be "no" right?
-
One of the harder things to accept as a teacher is that some kids will just never like math. That's fine though. I can cope.
What everyone *can* like (at least) is getting the right answer and knowing it's right. Knowing that yourself not needing anyone to tell you.
So I'm hoping we can at least get to that stage.
Right now I think she thinks I'm just making up geometry as I go and it's basically Calvinball.
@futurebird i was a kid like that, and i later got diagnosed with dyscalculia. The reason i didnt get diagnosed as a kid, was because i have very strong memory so i just memorized everything. So i could really struggle if a triangle was a little rotated, because it didnt fit the example i memorized.
-
We use the numbers consistently because I find using three letters is more confusing for most students.
eg ∠ABC = ∠BCA
vs. ∠3 = ∠2
Which do you find less confusing?
We could also do ∠B = ∠C but naming angles by single letter is a bad habit since there can be multiple angles at a vertex.
@futurebird what I find less confusing is the version I was taught. Whether that's because it works better for my brain, or because it's familiar, I do not know.
I'm used to seeing all labels being letters, but only the angles / vertices / lines relevant to the question. So on this one, because it's asking about angles, the angles would be labeled with letters by little arcs. I find the extra labels on the point confusing because we don't need to do anything with the points to answer the question.
Of course, the downside is that some people will get confused between angles and points, even with the arcs.
I'm pretty sure there isn't a single way of showing this that is easy for everyone. -
We use the numbers consistently because I find using three letters is more confusing for most students.
eg ∠ABC = ∠BCA
vs. ∠3 = ∠2
Which do you find less confusing?
We could also do ∠B = ∠C but naming angles by single letter is a bad habit since there can be multiple angles at a vertex.
Maybe it's just what you are accustomed to.
I normally expect the points to be named, so a line would be named e.g. AB.
The natural way to name an angle then would be something like AB∠BC, which is annoyingly long and thus led people to use greek letters.
-
@3TomatoesShort @EverydayMoggie @futurebird I was going to suggest paper modeling. I can’t calculate anything to save my life, but give me a concrete thing I can shape with my hands and things start to make sense. You mentioned compasses. Nobody has reliably convinced me they can do anything except make circles. The whole thing where you use them to make angles is deep magic that only wizards can perform.
@Bumblefish @3TomatoesShort @EverydayMoggie
"The whole thing where you use them to make angles is deep magic that only wizards can perform."
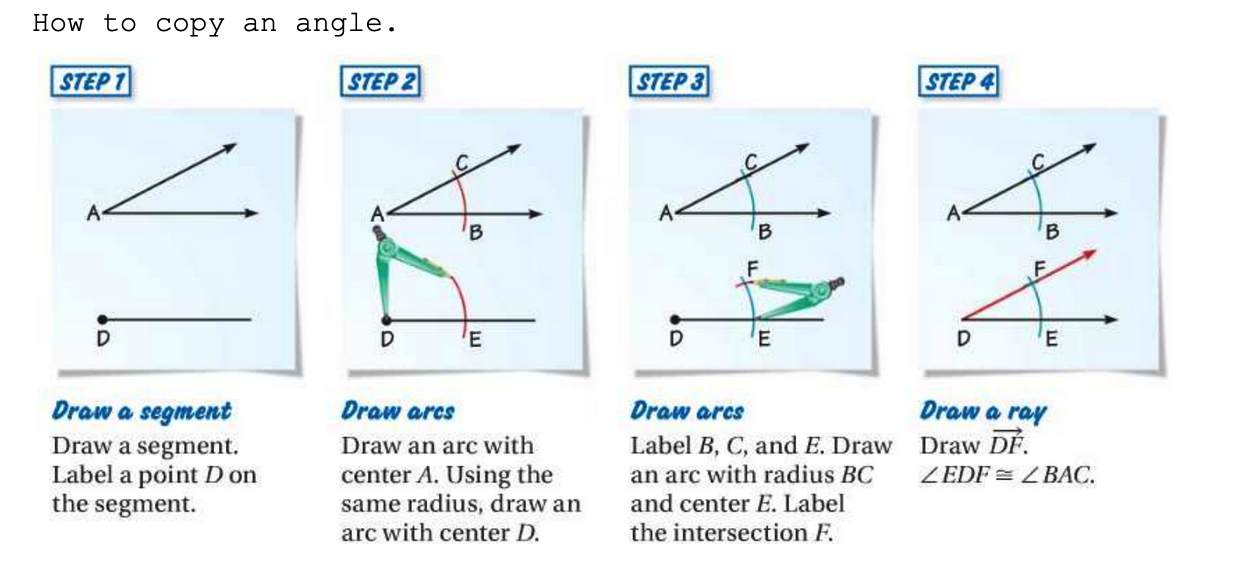
I've noticed that the angle construction is harder for students. Not just this one who's having extra difficulty, but all of them are a little mystified when I say "now we'll copy an angle" but there is some good intuitive geometry in this construction.
A compass isn't just for making circles. It's a fixed distance you can put wherever you want.
-
Maybe it's just what you are accustomed to.
I normally expect the points to be named, so a line would be named e.g. AB.
The natural way to name an angle then would be something like AB∠BC, which is annoyingly long and thus led people to use greek letters.
I've never seen it done that way before. But I do think it's more clear than using three letters since the vertex is repeated and stands out a bit more.
-
@futurebird what I find less confusing is the version I was taught. Whether that's because it works better for my brain, or because it's familiar, I do not know.
I'm used to seeing all labels being letters, but only the angles / vertices / lines relevant to the question. So on this one, because it's asking about angles, the angles would be labeled with letters by little arcs. I find the extra labels on the point confusing because we don't need to do anything with the points to answer the question.
Of course, the downside is that some people will get confused between angles and points, even with the arcs.
I'm pretty sure there isn't a single way of showing this that is easy for everyone.How do you name the vertices?
We could go with greek letters rather than numbers but I have tried this and students find it more confusing than the numbers.
I don't really think the issue this student has is due to labeling.
-
@Bumblefish @3TomatoesShort @EverydayMoggie
"The whole thing where you use them to make angles is deep magic that only wizards can perform."
I've noticed that the angle construction is harder for students. Not just this one who's having extra difficulty, but all of them are a little mystified when I say "now we'll copy an angle" but there is some good intuitive geometry in this construction.
A compass isn't just for making circles. It's a fixed distance you can put wherever you want.

@futurebird oh, no. This isn't obvious at all.
-
@futurebird i was a kid like that, and i later got diagnosed with dyscalculia. The reason i didnt get diagnosed as a kid, was because i have very strong memory so i just memorized everything. So i could really struggle if a triangle was a little rotated, because it didnt fit the example i memorized.
This is interesting. The student happens to be really good at memorizing things. And thinking back when a problem is rotated it really throws her.
Maybe we can work on doing things like first rotating the paper to a familiar position.