Is there a name for when someone thinks they are really bad at something (for example math) and they have learned not to trust their own intuition at all so they make really wild errors by second guessing themselves?
-
One of the harder things to accept as a teacher is that some kids will just never like math. That's fine though. I can cope.
What everyone *can* like (at least) is getting the right answer and knowing it's right. Knowing that yourself not needing anyone to tell you.
So I'm hoping we can at least get to that stage.
Right now I think she thinks I'm just making up geometry as I go and it's basically Calvinball.
@futurebird i was a kid like that, and i later got diagnosed with dyscalculia. The reason i didnt get diagnosed as a kid, was because i have very strong memory so i just memorized everything. So i could really struggle if a triangle was a little rotated, because it didnt fit the example i memorized.
-
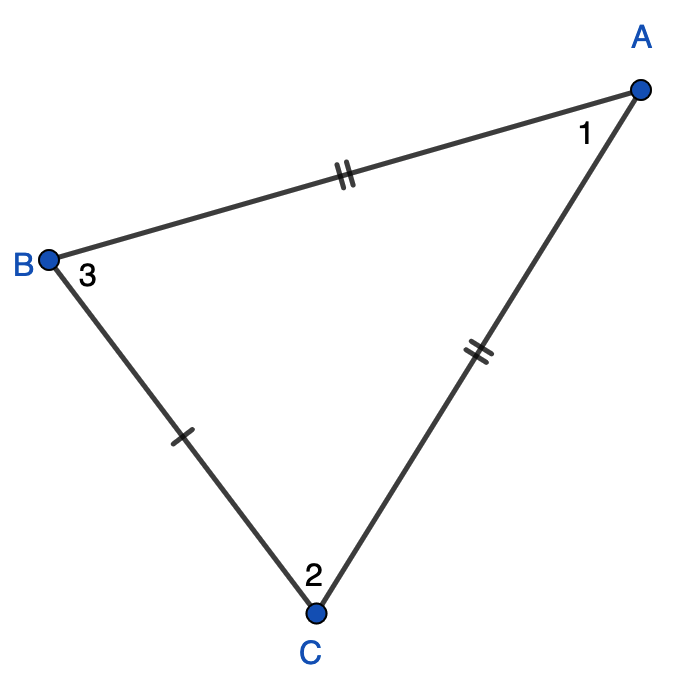
We use the numbers consistently because I find using three letters is more confusing for most students.
eg ∠ABC = ∠BCA
vs. ∠3 = ∠2
Which do you find less confusing?
We could also do ∠B = ∠C but naming angles by single letter is a bad habit since there can be multiple angles at a vertex.
@futurebird what I find less confusing is the version I was taught. Whether that's because it works better for my brain, or because it's familiar, I do not know.
I'm used to seeing all labels being letters, but only the angles / vertices / lines relevant to the question. So on this one, because it's asking about angles, the angles would be labeled with letters by little arcs. I find the extra labels on the point confusing because we don't need to do anything with the points to answer the question.
Of course, the downside is that some people will get confused between angles and points, even with the arcs.
I'm pretty sure there isn't a single way of showing this that is easy for everyone. -
We use the numbers consistently because I find using three letters is more confusing for most students.
eg ∠ABC = ∠BCA
vs. ∠3 = ∠2
Which do you find less confusing?
We could also do ∠B = ∠C but naming angles by single letter is a bad habit since there can be multiple angles at a vertex.
Maybe it's just what you are accustomed to.
I normally expect the points to be named, so a line would be named e.g. AB.
The natural way to name an angle then would be something like AB∠BC, which is annoyingly long and thus led people to use greek letters.
-
@3TomatoesShort @EverydayMoggie @futurebird I was going to suggest paper modeling. I can’t calculate anything to save my life, but give me a concrete thing I can shape with my hands and things start to make sense. You mentioned compasses. Nobody has reliably convinced me they can do anything except make circles. The whole thing where you use them to make angles is deep magic that only wizards can perform.
@Bumblefish @3TomatoesShort @EverydayMoggie
"The whole thing where you use them to make angles is deep magic that only wizards can perform."
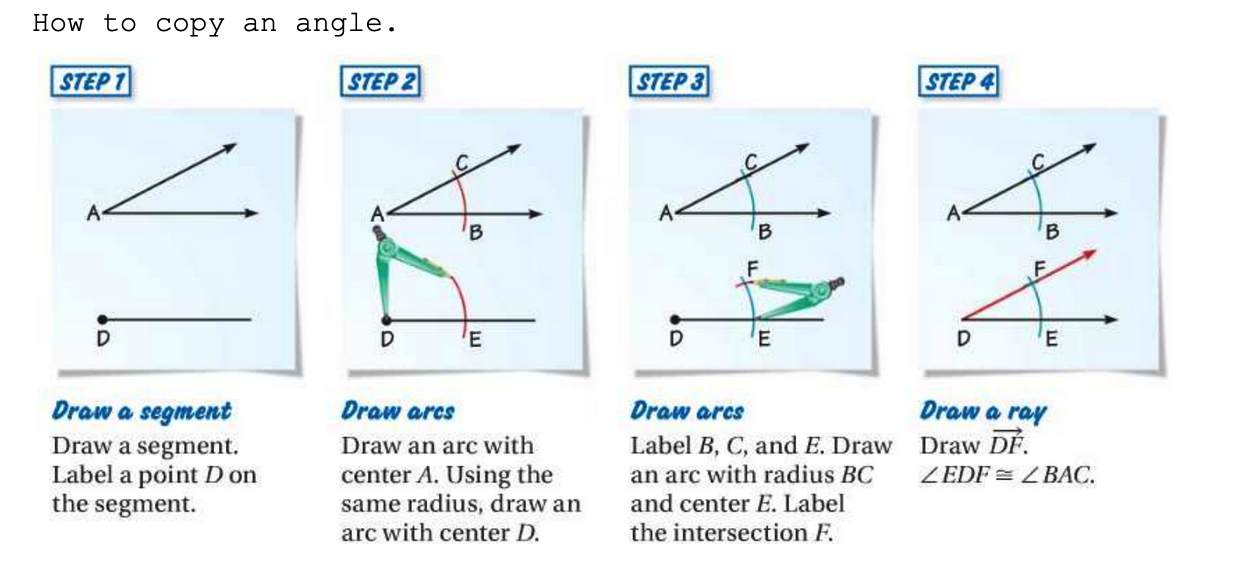
I've noticed that the angle construction is harder for students. Not just this one who's having extra difficulty, but all of them are a little mystified when I say "now we'll copy an angle" but there is some good intuitive geometry in this construction.
A compass isn't just for making circles. It's a fixed distance you can put wherever you want.
-
Maybe it's just what you are accustomed to.
I normally expect the points to be named, so a line would be named e.g. AB.
The natural way to name an angle then would be something like AB∠BC, which is annoyingly long and thus led people to use greek letters.
I've never seen it done that way before. But I do think it's more clear than using three letters since the vertex is repeated and stands out a bit more.
-
@futurebird what I find less confusing is the version I was taught. Whether that's because it works better for my brain, or because it's familiar, I do not know.
I'm used to seeing all labels being letters, but only the angles / vertices / lines relevant to the question. So on this one, because it's asking about angles, the angles would be labeled with letters by little arcs. I find the extra labels on the point confusing because we don't need to do anything with the points to answer the question.
Of course, the downside is that some people will get confused between angles and points, even with the arcs.
I'm pretty sure there isn't a single way of showing this that is easy for everyone.How do you name the vertices?
We could go with greek letters rather than numbers but I have tried this and students find it more confusing than the numbers.
I don't really think the issue this student has is due to labeling.
-
@Bumblefish @3TomatoesShort @EverydayMoggie
"The whole thing where you use them to make angles is deep magic that only wizards can perform."
I've noticed that the angle construction is harder for students. Not just this one who's having extra difficulty, but all of them are a little mystified when I say "now we'll copy an angle" but there is some good intuitive geometry in this construction.
A compass isn't just for making circles. It's a fixed distance you can put wherever you want.
@futurebird oh, no. This isn't obvious at all.
-
@futurebird i was a kid like that, and i later got diagnosed with dyscalculia. The reason i didnt get diagnosed as a kid, was because i have very strong memory so i just memorized everything. So i could really struggle if a triangle was a little rotated, because it didnt fit the example i memorized.
This is interesting. The student happens to be really good at memorizing things. And thinking back when a problem is rotated it really throws her.
Maybe we can work on doing things like first rotating the paper to a familiar position.
-
@Bumblefish @3TomatoesShort @EverydayMoggie
"The whole thing where you use them to make angles is deep magic that only wizards can perform."
I've noticed that the angle construction is harder for students. Not just this one who's having extra difficulty, but all of them are a little mystified when I say "now we'll copy an angle" but there is some good intuitive geometry in this construction.
A compass isn't just for making circles. It's a fixed distance you can put wherever you want.
@futurebird @3TomatoesShort @EverydayMoggie
intuitive…you keep using that word. I do not think it means what you think it means (to paraphrase the immortal Inigo Montoya) -
@futurebird oh, no. This isn't obvious at all.
If anyone has ideas to make the idea of copying an angle more obvious I would love it.
I've tried pointing out that it's basically copying a triangle too. You are duplicating the length of all three sides and thus you get the angle for free.
It's "Side Angle Side" ... but that seems maybe more confusing than just doing it a few times and feeling how well it works.
-
@futurebird @3TomatoesShort @EverydayMoggie
intuitive…you keep using that word. I do not think it means what you think it means (to paraphrase the immortal Inigo Montoya)@Bumblefish @3TomatoesShort @EverydayMoggie
OK let me try this one:
How would you use a compass to make a very pointy isosceles triangle like a wizard's hat? For a quilt or something.
-
@Bumblefish @3TomatoesShort @EverydayMoggie
OK let me try this one:
How would you use a compass to make a very pointy isosceles triangle like a wizard's hat? For a quilt or something.
@futurebird @3TomatoesShort @EverydayMoggie I wouldn’t. I’d use two rulers as god intended.
-
@futurebird @3TomatoesShort @EverydayMoggie I wouldn’t. I’d use two rulers as god intended.
@Bumblefish @3TomatoesShort @EverydayMoggie
Ok but try.
-
@Bumblefish @3TomatoesShort @EverydayMoggie
Ok but try.
@futurebird @3TomatoesShort @EverydayMoggie I got a circle.
-
@futurebird @3TomatoesShort @EverydayMoggie I got a circle.
@Bumblefish @3TomatoesShort @EverydayMoggie
Great use the center and the circle to make a pointy triangle.
-
@futurebird @3TomatoesShort @EverydayMoggie I got a circle.
@futurebird @3TomatoesShort @EverydayMoggie Oh wait if I lie it down and trace around it I got a…wait wait *that’s* got an angle . What’s going on here?
-
@Bumblefish @3TomatoesShort @EverydayMoggie
Great use the center and the circle to make a pointy triangle.
@futurebird @3TomatoesShort @EverydayMoggie Ok so where I’m holding the compass is a pointy triangle.
-
@futurebird @3TomatoesShort @EverydayMoggie Oh wait if I lie it down and trace around it I got a…wait wait *that’s* got an angle . What’s going on here?
@Bumblefish @3TomatoesShort @EverydayMoggie
OK now I'm confused what you have done. This is what I was expecting. But, people always surprise me.
-
@Bumblefish @3TomatoesShort @EverydayMoggie
OK now I'm confused what you have done. This is what I was expecting. But, people always surprise me.
@futurebird @3TomatoesShort @EverydayMoggie No that would not occur to me in a million years.
-
@futurebird @3TomatoesShort @EverydayMoggie Ok so where I’m holding the compass is a pointy triangle.
@Bumblefish @3TomatoesShort @EverydayMoggie
EXACTLY!
The legs of the compass are the same length (roughly) so it makes an isosceles triangle.
