Is there a name for when someone thinks they are really bad at something (for example math) and they have learned not to trust their own intuition at all so they make really wild errors by second guessing themselves?
-
@futurebird
Yeah l-r or r-l is the same but many kids would flip top-bottom or rotate.I think focusing on the results might help? If they go top/bottom the text will be upside down.
So "flip it so the edge with the text is *still* near you but the lighter side of the board is on top" maybe?
The "left right" makes me think of rotating since with 90 degree turns left and right matter?
-
@dahukanna @Bumblefish @3TomatoesShort @EverydayMoggie
That sounds like so much work to me.
If you want someone with two parts that are the same length that start at the same point they have to be on a circle. No need to measure anything.
@futurebird I‘ve no cognitive intuition for geometry, never been able to tell left from right, am a visual learner & can imagine an Apple+smell it+hear crunch when I bite into it, …
So validating a flat planer isosceles triangle needs deliberate cognitive effort, else i’m guessing based on “way wind blows” or my mood.As a digital Designer, developed systems that enable expressing visual scene by literally, mentally mathematically raytracing scene. POV ray was “heaven”- camera, lights, action!
-
One of the harder things to accept as a teacher is that some kids will just never like math. That's fine though. I can cope.
What everyone *can* like (at least) is getting the right answer and knowing it's right. Knowing that yourself not needing anyone to tell you.
So I'm hoping we can at least get to that stage.
Right now I think she thinks I'm just making up geometry as I go and it's basically Calvinball.
@futurebird My experience as a tutor and a teaching assistant in math-heavy subjects was that, while it's not everyone, there are a lot of kids who basically get the material but who need someone to occasionally encourage them that they're on the right track when they seize up and second-guess themselves.
The second-guessing can be useful in more advanced study if it's targeted appropriately. If I didn't know for sure that that diagram was supposed to represent Euclidean geometry, I *couldn't* actually say that the congruent angles followed from the symmetry of the triangle without further assumptions. (Maybe the metric space it's in doesn't share that symmetry!) Then, that student's suspicion of intuition would be warranted. It's just misfiring in situations where it's not.
-
@futurebird I‘ve no cognitive intuition for geometry, never been able to tell left from right, am a visual learner & can imagine an Apple+smell it+hear crunch when I bite into it, …
So validating a flat planer isosceles triangle needs deliberate cognitive effort, else i’m guessing based on “way wind blows” or my mood.As a digital Designer, developed systems that enable expressing visual scene by literally, mentally mathematically raytracing scene. POV ray was “heaven”- camera, lights, action!
That's interesting. I *also* have no sense of left or right. "you injured your left leg which one still hurts?"
But, this has always been a secret advantage in mathematics since seeing patterns backwards happens as fast as forwards.
I don't mind doing measurements but here is another shot at avoiding it:
An isosceles triangle is a pendulum. The distances are the same because it's the same string. If a pendulum could swing all the way around it would make a circle.
-
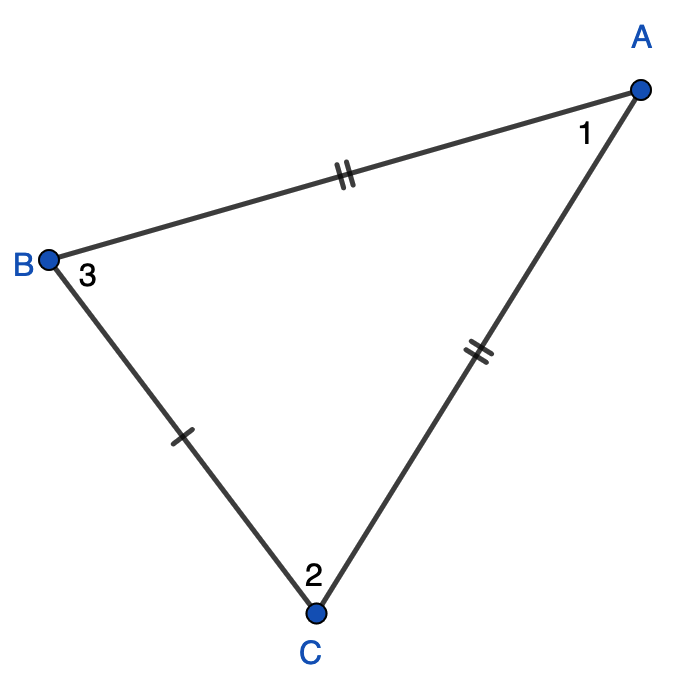
We use the numbers consistently because I find using three letters is more confusing for most students.
eg ∠ABC = ∠BCA
vs. ∠3 = ∠2
Which do you find less confusing?
We could also do ∠B = ∠C but naming angles by single letter is a bad habit since there can be multiple angles at a vertex.
@futurebird @jetlagjen I like the system where you have one arc in one angle then two arcs, etc., and an equal number of arcs for angles that are the same size.
But I guess if you are asking the student which angles have the same size, you can't use arcs in the problem.
Using letters to represent the line segments is the standard? I agree, naming angles by the combination of letters was confusing.
What if you use the dot of color to identify each angle? I guess that wouldn't photocopy well..
-
@futurebird My experience as a tutor and a teaching assistant in math-heavy subjects was that, while it's not everyone, there are a lot of kids who basically get the material but who need someone to occasionally encourage them that they're on the right track when they seize up and second-guess themselves.
The second-guessing can be useful in more advanced study if it's targeted appropriately. If I didn't know for sure that that diagram was supposed to represent Euclidean geometry, I *couldn't* actually say that the congruent angles followed from the symmetry of the triangle without further assumptions. (Maybe the metric space it's in doesn't share that symmetry!) Then, that student's suspicion of intuition would be warranted. It's just misfiring in situations where it's not.
That is too much second guessing. I mean... it's correct. I didn't say what kind of geometry or if this is on a plane. But ... that's too much.
-
@futurebird @jetlagjen I like the system where you have one arc in one angle then two arcs, etc., and an equal number of arcs for angles that are the same size.
But I guess if you are asking the student which angles have the same size, you can't use arcs in the problem.
Using letters to represent the line segments is the standard? I agree, naming angles by the combination of letters was confusing.
What if you use the dot of color to identify each angle? I guess that wouldn't photocopy well..
Using color to identify angles means you can't use it to show which ones are the same. Which is a great use for color if you don't have color blind students. (I don't at the moment but it's always in the back of my mind. )
-
That's interesting. I *also* have no sense of left or right. "you injured your left leg which one still hurts?"
But, this has always been a secret advantage in mathematics since seeing patterns backwards happens as fast as forwards.
I don't mind doing measurements but here is another shot at avoiding it:
An isosceles triangle is a pendulum. The distances are the same because it's the same string. If a pendulum could swing all the way around it would make a circle.
@futurebird
Physically rotated phone screen so that base of triangle was at x=0 & was 80% certain I was looking at an isosceles if base angles were actually, exactly identical.Re pendulum & isosceles, maybe being too literal but pendulum angle:
1. Could also represent an equilateral triangle.
2. Decreases to zero over time & is no longer an isosceles.I just realized that my default cognitive spatial map is x, y & z coordinates. So pendulum model example would not be intuitive heuristic.
-
We use the numbers consistently because I find using three letters is more confusing for most students.
eg ∠ABC = ∠BCA
vs. ∠3 = ∠2
Which do you find less confusing?
We could also do ∠B = ∠C but naming angles by single letter is a bad habit since there can be multiple angles at a vertex.
@futurebird
Skimming through is showing me that clearly I'm in the minority of your sample, but nonetheless:The three letter structure is what I grew up with, (but also/and so) was the easiest way to teach one of my kids. Line segments were intuitive to her, meaning the three letter system gave her all the angles on a figure without 'extra' labels. "Just follow the lines".
As a tangent to the thread, kudos once again to the effort you expend on your students.
-
@futurebird
Physically rotated phone screen so that base of triangle was at x=0 & was 80% certain I was looking at an isosceles if base angles were actually, exactly identical.Re pendulum & isosceles, maybe being too literal but pendulum angle:
1. Could also represent an equilateral triangle.
2. Decreases to zero over time & is no longer an isosceles.I just realized that my default cognitive spatial map is x, y & z coordinates. So pendulum model example would not be intuitive heuristic.
@dahukanna
1 and 2 are totally correct.An equilateral triangle is kind of isosceles triangle. One that works in three ways.
A line is a degenerate isosceles triangle with two right angles and a zero angle at the vertex OR two zero angels at the base and a 180 angle at the vertex. Probably better to call it a line.
Both of these are not always called isosceles but they are the natural extremes.
-
@futurebird
Physically rotated phone screen so that base of triangle was at x=0 & was 80% certain I was looking at an isosceles if base angles were actually, exactly identical.Re pendulum & isosceles, maybe being too literal but pendulum angle:
1. Could also represent an equilateral triangle.
2. Decreases to zero over time & is no longer an isosceles.I just realized that my default cognitive spatial map is x, y & z coordinates. So pendulum model example would not be intuitive heuristic.
@futurebird
I interpreted “pendulum could swing all the way around it would make a circle.” On z-axis, not y-axis -
@futurebird
Skimming through is showing me that clearly I'm in the minority of your sample, but nonetheless:The three letter structure is what I grew up with, (but also/and so) was the easiest way to teach one of my kids. Line segments were intuitive to her, meaning the three letter system gave her all the angles on a figure without 'extra' labels. "Just follow the lines".
As a tangent to the thread, kudos once again to the effort you expend on your students.
The three letters eg ∠ABC where B is the vertex are also what I learned and I hated the numbers when I first saw them. But, from experience I find they just work better. My little grumble about "but numbers are for measuring" and also "that's not how I learned it" are something I've gotten past.
I go with what helps the most students get it. Hence I don't use greek letters with ninth graders. Learning the new symbols at the same time was too much for some.
-
The three letters eg ∠ABC where B is the vertex are also what I learned and I hated the numbers when I first saw them. But, from experience I find they just work better. My little grumble about "but numbers are for measuring" and also "that's not how I learned it" are something I've gotten past.
I go with what helps the most students get it. Hence I don't use greek letters with ninth graders. Learning the new symbols at the same time was too much for some.
Also different populations of students have different needs. So, maybe I would switch if I thought it would work better with a new group.
I make a big deal about introducing the Greek letters in the spring when we start trig. This gives them time to learn how to write them.
So they do learn them by the end of the year? New symbols are a big deal and deserve space. Don't just spring them on people. I do find the numbers a little "janky" from a pure maths lens.
-
@futurebird
I interpreted “pendulum could swing all the way around it would make a circle.” On z-axis, not y-axisWell then you are making triangles in a different plane or triangular prisms maybe.
-
Also different populations of students have different needs. So, maybe I would switch if I thought it would work better with a new group.
I make a big deal about introducing the Greek letters in the spring when we start trig. This gives them time to learn how to write them.
So they do learn them by the end of the year? New symbols are a big deal and deserve space. Don't just spring them on people. I do find the numbers a little "janky" from a pure maths lens.
@futurebird
Solid thinking across the board, it sounds like you're the kind of teacher we'd all like to have.I'm curious, has your class size ever affected your decision to introduce 'one more thing', (read: Greek letters in this example)
A 15:1 classroom is a different environment than a 30:1.
-
@futurebird
Solid thinking across the board, it sounds like you're the kind of teacher we'd all like to have.I'm curious, has your class size ever affected your decision to introduce 'one more thing', (read: Greek letters in this example)
A 15:1 classroom is a different environment than a 30:1.
Absolutely. If I had 30 students I would not do the compass work. And that would be a big loss, but I would not be able to go around the room and help enough of them to hold it correctly, and keeping that many compasses sharp and ready to go is too much work.
Likewise teaching them to sharpen the lead on the compass is too much of a class time-sink. (although it's a very cool skill to have, so it make me sad)
I bring only working compasses with sharp lead to class.
-
@Bumblefish @3TomatoesShort @EverydayMoggie
OK pizza good to know.
Anyway. Connecting the center of a circle to two points like that is a great way to create an angle. When you copy an angle you are just cutting two pizza slices that are the same.
If the pizzas are the same size, and the distance between the points on the circle is the same. The angle at the top (center) is the same.
@futurebird @3TomatoesShort @EverydayMoggie But why use a compass to do that? Why not a ruler through the middle?
-
Using color to identify angles means you can't use it to show which ones are the same. Which is a great use for color if you don't have color blind students. (I don't at the moment but it's always in the back of my mind. )
@futurebird @jetlagjen ps this is the system of arcs I was talking about, to identify which angles are the same size. It works pretty well until you have a more complicated shape with many angles. Is there a name for this system?
-
@futurebird @3TomatoesShort @EverydayMoggie But why use a compass to do that? Why not a ruler through the middle?
@Bumblefish @3TomatoesShort @EverydayMoggie
Rulers are less precise than a compass. You could use a ruler if you wanted. But it will only be as precise as the markings you have made on the ruler.
-
@Bumblefish @3TomatoesShort @EverydayMoggie
Rulers are less precise than a compass. You could use a ruler if you wanted. But it will only be as precise as the markings you have made on the ruler.
@futurebird @3TomatoesShort @EverydayMoggie Not measuring anything, just using it to get a straight line. Could use any straight edge.