Is there a name for when someone thinks they are really bad at something (for example math) and they have learned not to trust their own intuition at all so they make really wild errors by second guessing themselves?
-
This is why basic math and esp. geometry were hard for me, but algebra was easy.
I had two math teachers in a room describe what they said was the same solution to the same problem, but I heard two different problems, solutions, and answers. They were both very exacting about what was the right answer, but became flustered when I brought up what didn't match up for me. In this thread, I've seen multiple notations for the same thing. To me, they are all different problems.
The things that are the same are what we are really trying to talk about.
-
The things that are the same are what we are really trying to talk about.
Ok. Sorry for being offbase.
-
Ok. Sorry for being offbase.
I didn't mean that you were off base. (Nor do I think you have anything to apologize for. )
It's fine to prefer a certain notation ... but the notation isn't really what it's about. I'm just suggesting that as a thread to pull to get past what isn't as important here.
I'm very particular about notation because I know it can be confusing as I explain here:
myrmepropagandist (@futurebird@sauropods.win)
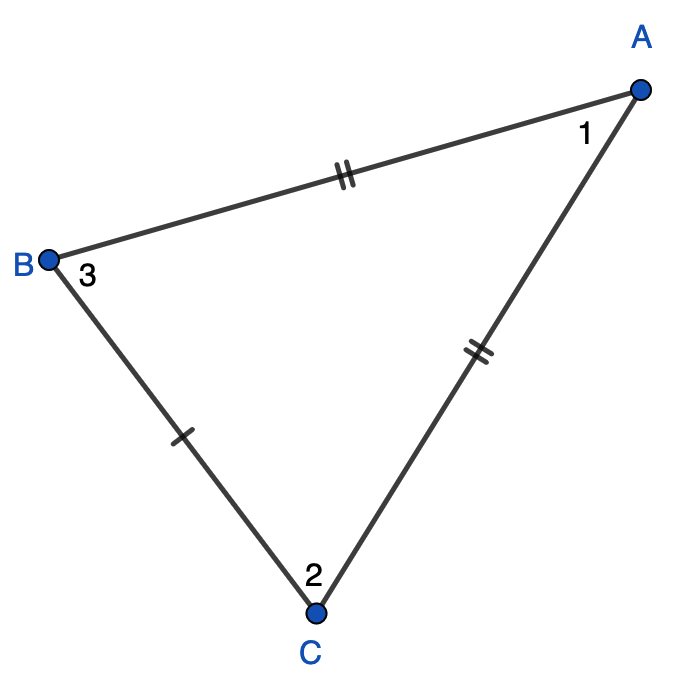
@jetlagjen@gts.phillipsuk.org We use the numbers consistently because I find using three letters is more confusing for most students. eg ∠ABC = ∠BCA vs. ∠3 = ∠2 Which do you find less confusing? We could also do ∠B = ∠C but naming angles by single letter is a bad habit since there can be multiple angles at a vertex.

Sauropods.win (sauropods.win)
-
@futurebird the more I think about, the more I think we may have used capital letters for vertices and lower case for angles as an unspoken convention. Like, maybe A, B, C for vertices and x, y, z for angles.
I've just checked my son's maths dictionary, and I can't see any vertices labeled in the angles or triangles sections.
It's entirely possible that it's any one (or several) of a hundred other things tripping up your student. Brains are weird and varied.A, B, C for vertices, α, β, γ for angles? But what would I know? It's all Greek to me!

Someone posted a link to this a while back; interesting in the context of the presentation discussion:
[#AltTextForMe - help!]
I thought it was obvious, but I'd seen in a Primary Maths Challenge (aimed at 9/10, 10/11 year old UK kids) … How many different isosceles triangles with whole number sides can you make from a loop of string 21 units long?
https://www.theguardian.com/science/2025/feb/17/can-you-solve-it-the-simple-geometry-question-that-fools-almost-everyone
: -
A, B, C for vertices, α, β, γ for angles? But what would I know? It's all Greek to me!

Someone posted a link to this a while back; interesting in the context of the presentation discussion:
[#AltTextForMe - help!]
I thought it was obvious, but I'd seen in a Primary Maths Challenge (aimed at 9/10, 10/11 year old UK kids) … How many different isosceles triangles with whole number sides can you make from a loop of string 21 units long?
https://www.theguardian.com/science/2025/feb/17/can-you-solve-it-the-simple-geometry-question-that-fools-almost-everyone
: -
A, B, C for vertices, α, β, γ for angles? But what would I know? It's all Greek to me!

Someone posted a link to this a while back; interesting in the context of the presentation discussion:
[#AltTextForMe - help!]
I thought it was obvious, but I'd seen in a Primary Maths Challenge (aimed at 9/10, 10/11 year old UK kids) … How many different isosceles triangles with whole number sides can you make from a loop of string 21 units long?
https://www.theguardian.com/science/2025/feb/17/can-you-solve-it-the-simple-geometry-question-that-fools-almost-everyone
:@hitsuyonai @jetlagjen @futurebird oh! Took me a bit. That’s just cruel
-
@hitsuyonai @jetlagjen @futurebird oh! Took me a bit. That’s just cruel
@cinebox @hitsuyonai @jetlagjen
It's a troll.
-
A, B, C for vertices, α, β, γ for angles? But what would I know? It's all Greek to me!

Someone posted a link to this a while back; interesting in the context of the presentation discussion:
[#AltTextForMe - help!]
I thought it was obvious, but I'd seen in a Primary Maths Challenge (aimed at 9/10, 10/11 year old UK kids) … How many different isosceles triangles with whole number sides can you make from a loop of string 21 units long?
https://www.theguardian.com/science/2025/feb/17/can-you-solve-it-the-simple-geometry-question-that-fools-almost-everyone
: -
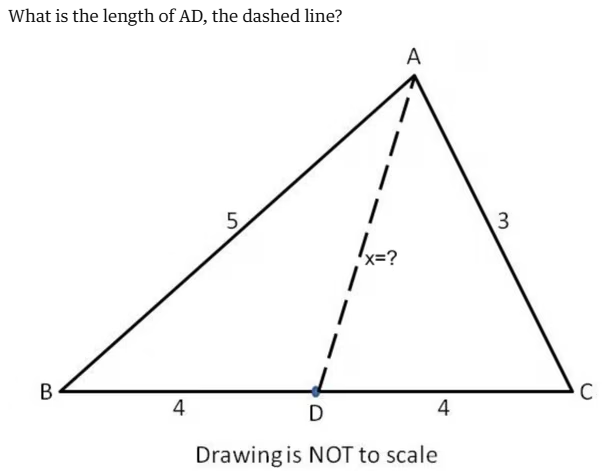
@futurebird @hitsuyonai @jetlagjen Honestly kinda hard to think about how to text-describe this when it's primarily(??) a visual troll-- that it's drawing the triangle as having 2-dimensional volume, when in fact it pointedly does not.
Does just saying "triangle" do that enough, and make a strong enough "this is in 2D" impression? should I go back and add more spacial descriptors, e.g. saying the segment goes "down" from A to D?
-
@futurebird @3TomatoesShort @EverydayMoggie Copy/paste works too…but this is basically how every conversation I have with math teachers goes, and I feel bad because I don’t get it, and it must be annoying for them all. In high school my last teacher just said I don’t actually need to know it and put me in a basic class where we learned to calculate rent on a low salary. Now that was easy to understand!
@Bumblefish @3TomatoesShort @EverydayMoggie
The reasoning you did to make this conclusion:
That’s a moray (@Bumblefish@mastodon.scot)
@futurebird@sauropods.win @3TomatoesShort@disabled.social @EverydayMoggie@sfba.social The opposite one will always be the same size.

mastodon.scot (mastodon.scot)
... means you can understand geometry and congruent triangles.
To know those "slices" are equivalent is "Side Angle Side"
I think you just need to learn to like the compass better as a way to deal with lengths. It can be very powerful I'll show you an example. Someone posted a nasty trick question on this thread. Thinking about it with a compass makes the trick vanish.
-
@Bumblefish @3TomatoesShort @EverydayMoggie
The reasoning you did to make this conclusion:
That’s a moray (@Bumblefish@mastodon.scot)
@futurebird@sauropods.win @3TomatoesShort@disabled.social @EverydayMoggie@sfba.social The opposite one will always be the same size.

mastodon.scot (mastodon.scot)
... means you can understand geometry and congruent triangles.
To know those "slices" are equivalent is "Side Angle Side"
I think you just need to learn to like the compass better as a way to deal with lengths. It can be very powerful I'll show you an example. Someone posted a nasty trick question on this thread. Thinking about it with a compass makes the trick vanish.
@Bumblefish @3TomatoesShort @EverydayMoggie
OK here is the trick question in the replies I show how to answer it with a compass.
Hitsu Yonai (@hitsuyonai@mastodon.online)
Attached: 1 image @jetlagjen@gts.phillipsuk.org @futurebird@sauropods.win A, B, C for vertices, α, β, γ for angles? But what would I know? It's all Greek to me! 😉 Someone posted a link to this a while back; interesting in the context of the presentation discussion: [#AltTextForMe - help!] I thought it was obvious, but I'd seen in a Primary Maths Challenge (aimed at 9/10, 10/11 year old UK kids) … How many different isosceles triangles with whole number sides can you make from a loop of string 21 units long? https://www.theguardian.com/science/2025/feb/17/can-you-solve-it-the-simple-geometry-question-that-fools-almost-everyone :

Mastodon (mastodon.online)
-
@futurebird @hitsuyonai @jetlagjen Honestly kinda hard to think about how to text-describe this when it's primarily(??) a visual troll-- that it's drawing the triangle as having 2-dimensional volume, when in fact it pointedly does not.
Does just saying "triangle" do that enough, and make a strong enough "this is in 2D" impression? should I go back and add more spacial descriptors, e.g. saying the segment goes "down" from A to D?
@gaditb @hitsuyonai @jetlagjen
I think some of the descriptions were fine. Those that mention it's not to scale. Maybe it's an example of when having the description is superior to seeing the image visually.
-
@futurebird @3TomatoesShort @EverydayMoggie Infinite spiral of isosceles triangles, just eyeballed
@Bumblefish @3TomatoesShort @EverydayMoggie
... are you a spider?